Blogia
4actdani

Función exponencial

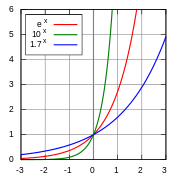
Funciones exponenciales para a = e (rojo), a = 10 (verde) y a = 1,7 (violeta).

La función exponencial (propiamente dicha) es una función matemática, que aparece además en muchas ecuaciones de la física. Esta función exponencial se caracteriza porque los valores de la derivada de dicha función son iguales al valor de la propia función (siendo la función exponencial la única función con esta propiedad). Toda funcion exponencial tiene por dominio de definicion el conjunto de los numeros reales. Además la función exponencial es la función inversa del logaritmo natural. Esta función se denota equivalentemente como:

x mapsto e^x qquad mbox{o} qquad x mapsto exp(x)

Donde e es la base de los logaritmos naturales.

En términos generales, una función real F(x) es de tipo exponencial si tiene la forma

F(x)=K cdot a^x

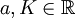siendo a, K in mathbb{R} números reales. Se observa en los gráficos que si a > 1 la curva será creciente.

Propiedades

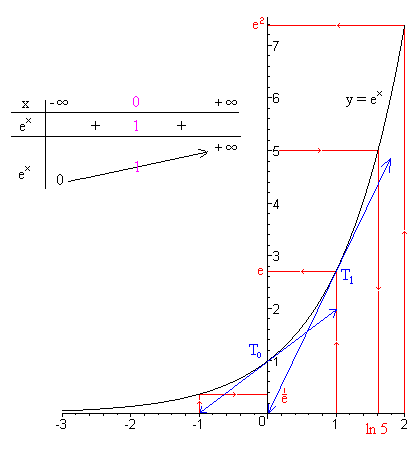
Todas sus propiedades provienen de las propiedades del logaritmo. Se llama (función) exponencial la función definida sobre los reales por x →ex.

  • La exponencial es la única función que es siempre igual a su derivada (de ahí su especial interés en el análisis, más precisamente para las ecuaciones diferenciales), y que toma el valor 1 cuando la variable vale 0.
  • La exponencial transforma una suma en una constante de la forma intrínseca del vertice de las siguientes ecuaciones:
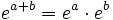
  • Relación adición-multiplicación: e^{a+b} = e^a cdot e^b
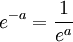
  • e^{-a} = {1 over e^a}
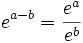
  • e^{a - b} = {e^a over e^b}
  • Sus límites en son lim_{xto -infty} e^x = 0, qquad lim_{xto +infty} e^x = infty
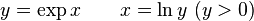
  • Inversa del logaritmo: y = exp x qquad x = ln y (y>0)
  • La tangente en x = 1, T1, pasa por el origen. La tangente en x = 0, T0, pasa por el punto (-1, 0).
  • La exponencial se extiende al cuerpo de los complejos, y satisface la sorprendente relación:

e^{i cdot t} = cos t + i cdot mbox{sen } t.

Un caso particular de esta relación es la identidad de Euler, conocida también como la fórmula más importante del mundo. Más generalmente:

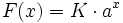
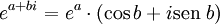
e^{a+bi} = e^{a}cdot(cos b + i mbox{sen } b)

0 comentarios